Der SourceCode ist nun unter der Adresse: https://github.com/ViceIce/sopralop verfügbar.
Mit freundlichen Grüßen
Michael Kriese
Überblick
Einführend zum Softwarepraktikum beziehungsweise als kurze Wiederholung
soll an dieser Stelle noch einmal ein Überblick über die Thematik
"Zweite geometrische Interpretation in der linearen
Optimierung" gegegeben werden.
Definition: In einem linearen Optimierungsproblem (im
folgenden kurz: LOP) wird eine lineare Zielfunktion der Variablen x1,
..., xn unter linearen Nebenbedingungen für diese Variablen
(Gleichungen oder Ungleichungen) maximiert oder minimiert.
Bei der zweiten geometrische Interpretation handelt es sich um
eine lineare Optimierung mit zwei Nebenbedingungen und beliebig vielen
Variablen.
Formal kann das wie folgt beschrieben werden:
| z = | c1x1 | + | c2x2 | + ... + | cnxn | = | max! (oder min!) |
| a11x1 | + | a12x2 | + ... + | a1nxn | = | b1 | |
| a21x1 | + | a22x2 | + ... + | a2nxn | = | b2 | |
| x1 | , | x2 | , ... , | xn | ≥ | 0 |
Um dieses Optimierungsproblem zu lösen, wird das Problem in den ℜ3 mit den Koordinaten u1, u2, u3 wie folgt transformiert:
| u1 | a11 | a12 | a1n | b1 | ||||
| u2 | = | a21 | x1 + | a22 | x2 + ... + | a2n | xn = | b2 |
| u3 | c1 | c2 | cn | z |
Das LOP hat dabei folgende Eigenschaften:
- Das Bild aller Punkte X = ( x1 ... xn )T ≥ 0 ist ein konvexer (mehrkantiger) Kegel K, der durch die Strahlen ( a1j, a2j, cj )T xj mit xj ≥ 0 ∀ j ∈ N erzeugt wird.
- Das Bild aller Punkte X, die die Nebenbedingungen Ax
= b erfüllen, ist die Gerade G:
u1 b1 b1 0 u2 = b2 = b2 + λ 0 , λ ∈ ℜ u3 z 0 1 - Der Lösungsbereich B des LOP wird auf den Durchschnitt K ∩ G abgebildet.
- Bei z = max! ist der "obere" Durchstoßpunkt von G durch den Kegel K zu bestimmen. Bei z = min! ist der "untere" Durchstoßpunkt von G durch den Kegel K zu bestimmen. ("oben", "unten" bzgl. u3-Achse!)
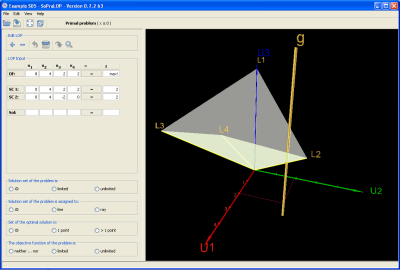
Hier setzt auch das Softwarepraktikum an. Mit den herkömmlichen
Mitteln war es gerade bei LOP's mit vielen Variablen bisher schwer bis
unmöglich, den konvexen Kegel zu visualisieren und damit die Lösung(en)
für das LOP zu bestimmen.
Hier unterstützt jetzt die vorliegende Software das Lokalisieren des
Lösungsbereiches bzw. der optimalen Lösung(en).
Dabei können folgende Fälle für den Lösungsbereich auftreten:
- Der Durchschnitt G ∩ K = ∅: Damit ist B leer, es existieren weder zulässige noch optimale Lösungen.
- Der Durchschnitt G ∩ K ist eine Strecke: zmin und zmax existieren.
- Der Durchschnitt G ∩ K ist ein Strahl:
- Es existiert zmax und zmin ist unbeschränkt oder:
- Es existiert zmin und zmax ist unbeschränkt.
Bei der Existenz von optimalen Lösungen gibt es folgende Möglichkeiten:
- Der Durchstoßpunkt der Geraden durch den Kegel liegt auf einer Seite des Kegels, die durch genau zwei Strahlen erzeugt wird: Die optimale Lösung ist eindeutig.
- Der Durchstoßpunkt der Geraden durch den Kegel liegt auf einer Seite des Kegels, die durch mehr als zwei Strahlen erzeugt wird: Es gibt mehrere optimale Lösungen.
Alle möglichen Fälle für die auftretenden Lösungen bzw. für den Lösungsbereich des LOP werden durch die Software dargestellt. Der Nutzer soll allerdings die Lösung selbst ermitteln und eingeben sowie die erkannten Fälle für die Lösung(en) bzw. den Lösungsbereich kennzeichnen.